Írta: G.D.Mutch

 

Az előző oldalakon szó volt arról, hogy a Joe cella méretei kritikusak a működés szempontjából. Ezen az oldalon megtudhatod, hogyan lehet meghatározni az egyes csövek méreteit - az átmérőjüket, magasságukat, falvastagságukat - egyszerű négyzetes mátrix használatával.

A Joe cella mátrix használata

Csoportosítsál egy mátrixot az 1. ábrán látható négyzet mátrix alapján úgy, hogy minden sor, oszlop és átló értéke pl. 255 legyen.

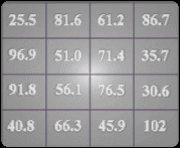
1. ábra. Egy négyzetes mátrix

 

Lényegtelen, hogy milyen módon adod össze az oszlopokat, sorokat vagy átlókat, azok mindig 255-öt adnak ki. Ezen kívül a négy belső cella ( 51.0, 71.4, 56.1 és 76.5) összege is 255. A négy legkülső sarok összege (25.5, 86.7, 40.8 és 102) szintén 255.

A mátrix további fontos tulajdonságai a következők:

 

Kiegyensúlyozatlan mátrix

25.5
45.9
66.3
86.7
30.6
51.0
71.4
91.8
35.7
56.1
76.5
96.9
40.8
61.2
81.6
102

Kiegyensúlyozott mátrix

25.5
81.6
61.2
86.7
96.9
51.0
71.4
35.7
91.8
56.1
76.5
30.6
40.8
66.3
45.9
102

1. táblázat. A kiegyensúlyozatlan és a kiegyensúlyozott mátrix

 

A négyzet mátrixban általában nem használunk tizedes jegyeket, mivel a természet nem használja az egész tizedes értékekeit vagy fraktáljait. De az 1. ábrán látható mátrix konkrét értékek alapján lett meghatározva. A saválló csövek méreteit általában a külső átmérőjük alapján adják meg, melyek értéke nagyon közeli az 1. ábra értékeihez. Az volt a cél, hogy ezzel a nagy pontossággal Te is megérthesd vagy módosíthasd ezeket az értékeket. Azonban ha a térfogatokra akarnám alkalmazni a mátrixot, akkor mindenképpen egész számokat használnék. Ezen kívül azt is megtehetjük, hogy eltávolítjuk a tizedesvesszőket a mátrix értékeiből, mikor a mátrix műveleteket végezzük és visszatesszük, mikor a számításokkal végeztünk.

 

A csövek értékei

Ha a fenti értékeket egyszerű milliméter alapú koordinátarendszerben használjuk, akkor ezeket az értékeket alkalmazhatjuk az átmérőkre, hosszakra és a csővastagságokra. A Joe cellában általában négy cső van, így négy értékre van szükségünk, ezért a mátrixnak 4 * 4-esnek kell lennie. Mivel a háromdimenziós térfogat értéket is használjuk, így mindegyik értéknek az X és az Y koordinátán, valamint az átlókban is jelen kell lennie.

 

A mátrix értékeinek használata

Az 1. ábrán látható mátrix bal átlójának használatával a következő értékeket kapjuk:

 

Miért a bal átlót használjuk?

A háromdimenziós univerzum természetes rendje az, hogy két erő hat egymásra. A három lehetséges állapot a differenciált összegzési pont, a kiegyensúlyozott nulla pont vagy ennek a két ellentétes erőnek az egyensúly pontja lehet. Ahhoz, hogy valami létezhessen, jelen kell lennie az X síkon ugyanúgy, mint az Y síkon. Mikor ezek a két erők találkoznak és egymás összegének kombinációit alkotják, akkor létrehozzák a Z síkot. Mikor két természetes erő összeadódik, akkor az eredő energiának valahová el kell jutnia, így a Z síkban jelenik meg valamilyen szögben. Ekkor válik a kétdimenziós háromdimenzióssá. Ez nyilvánvaló a mátrixból is: mikor az X és Y síkok metszik egymást, akkor létrehozzák a Z síkot is. A mozgást (mátrixot) kétdimenziós papíron ábrázolva a háromdimenziós teret is feltérképezhetjük. Gondolom, J. R. R. Searl professzor ezért használta szintén a bal átlót. A két háromszög felének tükrözésével a teljes mátrixot kiegyensúlyozhatjuk.

 

A csövek átmérői

A fenti átmérő értékeket közvetlenül milliméterekké alakíthatjuk, így a csövek átmérői ezek szerint:

 

A csövek hossza

Már tudjuk a mátrix sor értékét: 255. Ezt mint konstans hosszat használhatjuk a csöveknél, azaz minden egyes cső hossza:

 

A csövek vastagsága

Minden egyes cső falvastagsága a mátrix átlóértékeinek hányadosából származtatható. A legkisebb átmérőjű csővel kezdve a következő értékeket kapjuk:

2. ábra. A csövek falvastagságának értékei

 

A falvastagságok értékeit átlagolhatjuk, s ekkor ezt az átlagértéket használhatjuk minden cső esetében: (5 + 2 + 1,5 + 1,3 ) / 4 = 2,45 mm.

 

A legtöbb saválló cső konstans falvastagsággal rendelkezik, mint pl. 1,5 mm, 1,75 mm, 2,0 mm stb. Esetleg kísérletezhetsz különböző értékekkel vagy használhatod az átlagos értékeket is. Van egy másik állandó is, mely a hipotetikusan következő cső értékéből származik. Ezt mutatja a 3. ábra.

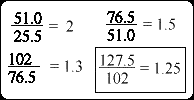
3. ábra. A következő cső méretéből származtatott hipotetikus érték (1,25)

 

A 127,5-es érték a feltételezett következő cső mérete, melyet egy nagyobb méretű mátrix esetén kapnánk. (Ez a nagyobb mátrix nincs feltűntetve ezen az oldalon.)

Ha használnánk a következő feltételezett csövet, akkor a következő arányokat kapnánk:

Ezt a feltételezett következő csövet csak azért említettem meg, mert lehet, hogy szeretnél több csőből álló cellát is készíteni.

 

A frekvencia

A mátrix sorainak összege 255.

Az értékek teljes összege: 4 * 255 = 1020

Ezt az értéket átalakíthatjuk Hertz-be, hogy megkapjuk a frekvenciát:

Ez a cella talán 1020 Hz-es frekvenciájú impulzusokat ad ki?

Ezt érdemes lenne kipróbálni a jármű gyújtótekercsének egyik harmonikusát használva. Lehet, hogy a matematikailag behangolt cella jobban vagy esetleg rosszabbul működik együtt a gyújtótekercs rezonanciafrekvenciájával?

 

Emlékeztetők

Mindegyik négyzetes mátrix két háromszögből áll, ezek alkotják a teljes négyzetet. A felső háromszög a tükörképe/ellentettje az alsó háromszögnek. A háromszögeket rendszerint a bal átló választja el egymástól. Ez a tükrözés nem mindig nyilvánvaló a mátrixoknál. Mikor egy kiegyensúlyozatlan négyzetes mátrixot használunk, akkor a jobb felső háromszög értékeinek összege mindig nagyobb a bal alsó háromszög értékeinek összegénél addig, míg ki nem egyensúlyozzuk a mátrixot.

 

Összegzés

Az 1. ábrán látható mátrix értékeinek használatával meghatározhatjuk a következőket:

Cső
Külső átmérő
Hossz
Falvastagság
Belső térfogat
1
25,5 mm 
255 mm 
5 mm 
48116 mm3 
2
51,0 mm 
255 mm 
2 mm 
442410 mm3 
3
76,5 mm 
255 mm 
1,5 mm 
1081943 mm3 
4
102,0 mm 
255 mm 
1,3 mm 
1978804 mm3 

2. táblázat. A Joe cella méretei az 1. ábrán látható mátrix alapján

 

Az 1. ábrán látható mátrix a Joe cella térfogatára is használható, de ezt másokra hagyom. Remélhetőleg az itt ismertetett mátrix elég egyszerű ahhoz, hogy bárki megérthesse.

 

Az eredeti anyagot angol nyelven itt olvashatod.

 

Lajos a következő gondolatokat fűzte a számításokhoz:

A Joe cella elméleti tanulmányozásánál a következő összefüggéseket vettem észre.

Miután tanulmányoztam a cella felépítését, és elolvastam a kapcsolódó írásokat, észre vettem hogy a méretezési instrukciókba hiba csúszott. Vizsgálódásomat az ezen az oldalon leírt "a cella méretezése kritikus" mondat indította el nálam, így hát visszamentem az eredeti, bár hiányos és nehezen értelmezhető rajzhoz. A rajzot a neten találtam, kinyomtattam és saját gondolataim szerint vizsgálgattam. Van itt egy méret és térfogat táblázat, amiben én emilyen összefüggést nem találtam, így hát elkészítettem a saját méret és térfogat táblázatomat és meglepő eredményeket kaptam.

A Joe cella méretezéséhez én is mátrixot használtam, de abban a kiinduló szám nem 25,5 mm, hanem egy coll, vagy inch, ami 25,4 mm. A mátrix így is működik, igaz az oszlopok összege 10 inch-re, vagyis 254 mm-re változtak, így a négycsöves Joe cella méretei az eredetileg megadott 1", 2", 3", és 4"-ra (inch-re) változtak. A megadott méretek alapján a következő gondolatok alapján haladtam tovább.

Mint tudjuk, a gyakorlati megvalósítás és az elmélet kicsit mindig eltér egymástól, így hát figyelmen kívül hagytam pár dolgot, és csak az összefüggéseket kerestem. Következtetéseket nem tudok levonni, mert sem fizikus, sem matematikus nem vagyok, de az eredmények szerintem érdekesek. Tehát a következő dolgokat nem vettem (egyenlőre) figyelembe: A cella csöveinek a falvastagságát (0 mm), valamint a szerkezetbe bekerülő távtartók, tömítések térfogatát (nulla "köb" milliméter).

Ezen számítások alapján a belső, azaz az 1"-os cső belső átmérője 25,4 mm, hossza 8" vagyis 203,2 mm. Hogy miért 8" ? Mert a rajzon így van megadva. Ezek alapján az én általam számolt 1-es cső térfogata (a Pi 3,14 ): 16206,419 mm3. (A Pi érték pontossága szintén elhanyagolható az összefüggések kimutatása szempontjából.) A 2-es cső 2" vagyis 50,8 mm hossza 203,2 mm, térfogata az egyes cső átmérőjének kétszerese, hossza 203,2 mm, térfogata háromszorosa az 1"- os csőének, vagyis 48619,257 mm3. A négyes 4"-os 101,6 mm-es külső, borító cső hossza 10" vagyis 254 mm térfogata 81032,096 mm3 ez a térfogat pontosan a 1.-es cső térfogatának (5X) ötszöröse, a 2.-es cső térfogatának (2,5X) kettőegész-öttized szerese, a 3.-as cső térfogatának (2X) kettőszerese. (Lényeges-e, hogy 2X2,5 = 5 ?)

Tovább vizsgálódva a térfogat összefüggésekben, megvizsgáltam, ha a 4.-es 4"-os cső hossza is 8", vagyis 203,2 mm lenne, milyen térfogat jönne ki, és így 64825,676 mm3 kaptam, ami az első számítás után számolt érték (81032.096 mm3) ötnegyede (5/4), megfordítva a mostani számítás szorozva 1,25.-el egyenlő első számítás (64825,676X1,25 = 81032,096).

Érdekes az is, hogy az 1.-es cső térfogata pontosan négyszer van meg a 4.-es cső térfogatába 203,2 mm-el számolva (64825,676:16206,419 = 4), és ötször, ha 254 mm-el számolunk (81032,096:16206,419 = 5). Ha kivonjuk egymásból a két eredményt, akkor az 1.-es cső térfogatát kapjuk. Hasonló eredményeket kapunk a többi (2.-es, 3.-as ) cső esetében is. Meglepő eredményt adott a záró fedél területének számítása is, mivel a záró lemezek területe tízszerese négyzetmilliméterben a 4.-es 4"-os cső térfogatának
(10"-os , 254mm-nél) köbmilliméterben meghatározott értékénél (101,6mm osztva kettővel, négyzetre emelve, szorozva 3,14 = 8103,2096), (8103,2096X10 = 81032,096) Hmm érdekes!

Nem tudom, merjek-e következtetni bármire is, mindenesetre a számok magukért beszélnek!

Nézzünk ezt meg a gyakorlatban! Itt már kellenek a távtartók, tömítések, és a csöveknek is van falvastagsága. Tételezzük fel, hogy az elméleti berendezésünk a fent leírt méretezések alapján működik, és ha így meglehetne építeni (ami persze lehetetlen), akkor 100 %-os. Ha bármit konstruálunk, az általában az elméletinél kisebb hatásfokkal fog a gyakorlatban működni, tehát törekedjünk megtartani az arányokat. Most itt arra gondolok, hogy mielőtt megépítenénk a "ketyerét", vegyük figyelembe, mit is teszünk bele. A leírtak alapján alufólia vastagságú Joe cellát kellene építeni, de ez biztos nem lenne tartós darab. A távtartók térfogatával az 1.-es és 2.-es csőnél, a 2.-es és 3.-as csőnél variálhatunk, ez 6-6 db távtartó, az 1.es csőbe belesajtolt menetes szárban végződő rúd térfogatával, valamint a 4.-es csőbe az 1.-es csőből kijövő menetes szár, valamint az ezekhez tartozó szigetelő tömítések térfogatával játszadozhatunk, hogy a térfogat arányok csak minimálisan, a lehető legkisebb mértékben térjenek el egymástól. Jó lenne valamilyen számítógépes program, ami pillanatok alatt kiszámolná a megfelelő méreteket, de addig próbálkozhatunk kiszámolni!

Na én most neki fogok számolni!

 

 

A Joe cella felépítése MenüJoe cella videók

 

Utolsó frissítés dátuma: 2006. augusztus 16.